古典密碼學已經被電腦打爆了,但這跟它重不重要一點關係都沒有。
── 我的資安導師總是這樣嘮叨著……
最近重新改寫以前的Blog,終於理解這句話的意涵。舉凡近代加密演算法,多為古典密碼學手段的組合,只不過以前人力與能力都不及。
比方說你不會想把16個字母放進一個矩陣中,每個查表代換10次,再每行平移幾個單位,然後各別乘上一個矩陣,最後再和別的矩陣做XOR邏輯判斷。
Welcome to modern cryptography
這也太繁瑣了,正常人才不會想圈圈畫畫這些詭異的流程。不過,若將這些細項拆開來看,平移對應到移項式密碼,代換跟替換式密碼有關,矩陣運算則是來自希爾密碼,XOR就比較特別了些,但兩無關序列間的運算,可讓人追溯至維吉尼亞密碼的金鑰概念,這些都屬於古典加密的範疇。所以若想踏入近代密碼的殿堂,古典密碼當為一個必經的前哨站,助於釐清算法本身的原理與優劣勢。
基本概念
明文 (Plain text)
即是要加密的內容,不過,文不一定單指文字,也包含了圖片、音樂、各式各樣的檔案都可以當作明文。又因為明文的單字為Plain text,在密碼學上,我們常常用大寫字母P來表示它。
密文 (Cipher text)
呃…顧名思義,加密後的結果,跟明文一樣能有很多種型式,比方可以把圖片加密成另一張圖片。因為單字是Cipher text,所以用C來表示它。
金鑰
有些加密算法會有的另一個參數,當然它也不是真的鑰匙,可能為一組文字序列,演算法把它和明文做處理後產出密文。
絕對安全
若我們說一個演算法是絕對安全的,代表即便有無限的時間、無限的資源,也沒辦法靠蠻力破解該算法。
計算安全
若我們說一個演算法是計算安全的,則是說靠蠻力攻擊,我們確實能破解這個算法,不過得付出極為大量的時間。
加密算法
它會吃進明文吐出密文,接下來的重頭戲。
一個好的加密算法應至少具備這兩項條件:
- 混淆(confusion)
讓密文與金鑰的關係盡可能複雜,排除掉一些不該存在的弱金鑰,以防攻擊者透過觀察密文就能破解算法。
- 擴散(diffusion)
擴散是指即便明文間只有一丁點的不同,產生出的密文也要大不相同。
加密工具
1.密碼棒 (Scytale)

取布條將其纏繞於木棒上,橫向寫下明文後取下布條。解密時,必須取得相同直徑的木棒。
2.卡爾達諾漏格板 (CardanGrille)

依照漏格書寫明文以及觀看明文。
3.一次性密碼本
使用亂數產生的一本加密用密碼本,可以把它想成一組金鑰,每當要產生明文時,將明文與密碼本的內容相加,如明文中的字母C (3)與密碼本的字母 X (25),3+25=28,因為28超過了26個英文字母,而對28取餘數得2,即得加密完成的密文字母B。
一次性密碼本有三個限制:
- 確定密碼本是由隨機產生的
- 密碼本必須只能使用一次
- 因為要與明文相加,密碼本至少要與明文一樣長
加密算法
凱撒密碼
凱撒密碼出自羅馬軍事家尤利烏斯·凱撒,遽聞其當年曾用此與將領們進行秘密通訊。
凱撒密碼的流程並不難,因為當時的敵人多是目不識丁的。
已知明文字母P,引入一個參數K,得出密文 C = (P + K)mod 26
例如 ABCDEFGHIJK,在K=3時,得出密文DEFGHIJKLMN。(K=3是最初的凱撒密碼)
解密時 P = (C - K)mod 26。
由於凱撒密碼只是對英文字母進行簡單的代換,我們可以透過分析各個字母出現的頻率推斷明文,比方說英文書寫上最常出現的字為 E ,我們便可以猜測密文中出現最多次數的英文字母是 E 的代換,藉此得出 P 與 C 的關係。
由於這個方法主要是觀察英文字母使用的頻率,故又稱為頻率分析法,對於簡單的字母代換,頻率分析往往是有效的手段。
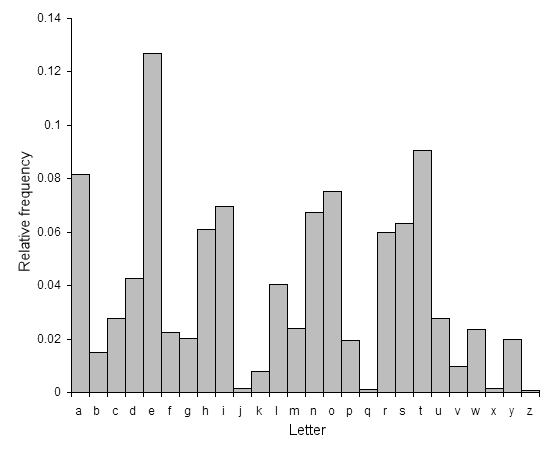
也因其架構簡單,現今電腦已能用暴力法輕易破解,故鮮少在資安領域出現了,不過仍常在字謎遊戲見到它的蹤影,比如ROT-13。
希爾密碼
使用矩陣進行加密,由密文構成的密文矩陣C = KP,其中P為明文構成的明文矩陣,K為密鑰矩陣,密鑰矩陣須為可逆才可供解密

希爾加密避開了頻率分析攻擊,然而在已知明文的情況下,可透過逆運算求得金鑰,無法保證安全性。
路由加密
近似於密碼棒,採用直書橫寫的方式進行加密。
單字母替換密碼
與凱撒密碼同為單字母取代的概念。將26個英文字母分別做對應,比如A對應C,B對應F,替換不受限於特定規則,也不要求有跡可循,純粹是做出26個字母的明文密文對應表,以供加密與解密時使用。
我們能運用洗牌演算法很輕易的產生出單字母密碼替換表。儘管其複雜度(26!)遠遠高於凱撒密碼,但明文字母與密文字母仍屬一對一對應,同樣易受頻率分析攻擊破解,當然也擋不住電腦暴力搜尋。一個可行的解決方案是:在明文中添加一些無關緊要的擾亂字母,或是一份明文使用多個表進行對應。
維吉尼雅密碼
維吉尼亞密碼主要是透過查表進行字母的轉換

上圖其實是由26個凱撒密碼構成的。
- 第一行為字母位移 0 位的凱撒密碼 ABCDEFG…(即原順序)
- 第二行為字母位移 1 位的凱撒密碼 BCDEFGH…
- 第三行為字母位移 2 位的凱撒密碼 CDEFGHI…
- ……以此類推
維吉尼雅密碼首先引入了金鑰的概念,假設要加密ABCDEFG,使用密鑰CIP。首先,先將密鑰長度補至和明文一樣長,例如:
CIPCIPC
接下來,取第A行第C列得A(實際上就是雙重的凱撒密碼),取第B行第I列得J…取第G行第C列得I,如此完成加密。
由於引入了金鑰這個變換要素,我們在明文上做了兩次變換,普通的頻率分析不適用在維吉尼亞密碼,只要確保金鑰不過度重複(如配合一次性密碼本),維吉尼亞密碼是足夠安全的。
攻擊類型
1.僅知密文攻擊
攻擊者在只知道密文的情況下試圖求得明文或金鑰。
2.已知明文攻擊
攻擊者在知道部分明文與密文配對的情況下試圖破解。
3.選擇明文攻擊
公開加密器,攻擊者可以自由輸入明文及得到該明文的密文,藉此試圖破解算法。
儘管選擇明文攻擊攻防上看似不合理,但在近代密碼學中,十分強調在公開演算法的情況下,還能保證安全的才是優秀的演算法。
用最最直觀的角度來看,要做一個加密流程很容易,我們可以有很多把金鑰,再搭配各式各樣的函式打造自己的流程,反覆做個幾十次,甚至幾百次,雖然它的效率不怎麼樣(其實這是個大問題),但只要流程與金鑰不外洩,這個演算法理論上牢不可破。
但是換個立場,如果我們是使用者,今天開發者送來了一個自行開發的加密算法,就像上述的流程一樣繁瑣,明文與密文間根本找不著對應。乍看之下,這個加密器可說是有效的,但是,如果它擁有一把尚未發現的萬用鑰匙呢?或是說這幾百道的換算其實能被規約成兩三條式子,是不是藏著一些未發現的漏洞或暗門?。
對這些疑問,身為使用者的我們無法斷言,至於開發者?如果知道,那他便是最危險的攻擊者。若連開發者也不能肯定,這個算法隨時都有可能會爆炸,更糟糕的是,爆炸按鈕還是我們自己觸發的。
確實,加密流程較少人知道會較安全,但暗門也較難找出。對這種保護機密資料的演算法,應該公開給全世界敲敲打打,把流程都公開,如果還是牢不可破,這個算法的安全性便有全球資安好手掛保證,像是近代算法中的AES、A5/1,便透過各方人才的審核,不但確保了使用上了安全性,也建立出自己的好口碑。